This is a brief overview of the main features of the MPI-AMRVAC software package.
Structure
This software has to be configured, preprocessed, and compiled into a single main executable program, amrvac which can be run on multiple processors using MPI. MPI-AMRVAC will initialize and advance the unknowns, and perform automated grid refinement to follow all details of the (possibly shock-dominated) flow. The program is split into several logical parts, and heavily uses Fortran 90 modules and dynamic allocation.
Once the configuration and compilation are done, amrvac can advance the solution in time, or can be used to convert previously produced data files to specific other formats for visualization. The data itself will be saved into .dat data files, which each contain a single snapshot of all grids and their unknowns in time, which can be used for eventual restarts. Besides these snapshots, the code can write output in a number of formats, which can directly be visualized with e.g. Paraview or Visit.
Source Language and Compilation
The *.t source files of AMRVAC are written in dimension independent notation, known as the LASY syntax. A suitably modified (and also simplified) version of the VAC Pre-Processor, VACPP translates the source code files to Fortran 90.
Equations
In general, MPI-AMRVAC aims to solve a system of (primarily hyperbolic) partial differential equations written in conservation form, with optional source terms on the right hand side:
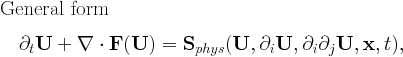
See equations for more detail.
Grid and Boundary
The following types of finite-volume grids are supported:
- Cartesian 1D, 1.5D, 2D, 2.5D, 3D
- Cylindrical 2D, 2.5D, 3D
- Polar 2D, 2.5D, 3D
- Spherical 2D, 2.5D, 3D
The slab, cylindrical or spherical grids differ in the definition of volumes and surfaces for the grid cells, and there are some extra terms in the equations, like the p/r term in the radial momentum equation for hydrodynamics. These are defined in the addgeometry subroutines for each AMRVACPHYS module. For polar grids the same geometrical source terms are used.
The boundaries are represented by ghost cells around the physical mesh. Of course, for a grid-adaptive computation, internal boundaries are handled appropriately, and the user is expected to interfere only with the physical domain boundaries, which represent 2, 4, or 6 regions depending on the dimensionality (1,2 or 3). The boundary types are defined for each region and each variable separately. The following boundary types are available:
| Type | Value of the ghost cell |
|---|---|
| periodic | Copied from opposite edge of the mesh |
| symm | Reflected from closeby mesh cells |
| asymm | Reflected from closeby cells and multiplied by -1 |
| cont | Copied from mesh cell next to the ghost cell |
| special | Defined by the specialbound subroutine in AMRVACUSR module |
The pages on discretization and axial coordinates provide further information.
Spatial Discretization
In MPI-AMRVAC, most discretizations are shock capturing conservative numerical schemes. A non exhaustive list is given by:
| Name | Description |
|---|---|
| cd4 | 4th order central difference scheme |
| tvdlf | MUSCL type TVD-Lax-Friedrich |
| tvdmu | TVD-MUSCL with Hancock predictor |
| tvd | One-step temporally 2nd order TVD |
| hll | Harten-Lax-van Leer (HLL) solver |
| hllc | Harten-Lax-van Leer-Contact (HLLC) solver |
| hlld | Harten-Lax-van Leer-Discontinuities (HLLD) solver |
| fd | conservative finite differences, up to fifth order with MP5 reconstruction |
In multidimensional MHD calculations the divergence of the magnetic field may become significantly different from zero. This may cause numerical instability or inaccurate results. There are several source-term options to fix this problem. E.g., Powell non-conservative source terms, which are proportional to div B, can be used to stabilize, and to improve the accuracy for any of the methods. We also provide several variants of the Dedner GLM scheme.
See methods for a more detailed description.
Temporal Discretization
With the finite volume methods, second order accurate explicit time integration can be obtained by predictor-corrector and multistep Runge-Kutta type discretizations. See time_discretization. In finite differences, the overall accuracy can go up to fourth order using the appropriate temporal discretizations. The more important ones are:
| Name | Description |
|---|---|
| onestep | 1st order Euler scheme |
| twostep | 2nd order predictor-corrector schemes |
| threestep | 3rd order (TVD) Runge-Kutta |
| fourstep | rk4 allows for selecting 4th order Runge-Kutta (classical) |
| fourstep | ssprk4 is a 3rd order, strong stability preserving four step Runge-Kutta |
| fivestep | ssprk5 is 4th order, strong stability preserving five step Runge-Kutta |
The time step can be adjusted dynamically to satisfy the stability criteria.